This special guest blog post by Linnart Felkl presents a case study where he used a conveyor simulation model for verifying a conveyor layout. Linnart chooses AnyLogic to build this model because he finds AnyLogic to be a convenient modeling software for controlling material flow routings. A model of this kind allows for testing competing material flow routing logic in the early stages of warehouse intralogistics design.
There are different types of simulation methods available. In this article, I apply discrete-event simulation to model the dynamic behavior of a conveyor system intersecting a storage yard. Discrete-event simulation facilitates an appropriate methodology for analyzing complex processes, i.e. sequences of events. Most importantly, simulation models can consider dynamic system interactions by reflecting interdependencies between model entities that other methods fail to consider. Other methods, such as e.g. mathematical programming, cannot or only at infeasible effort, consider such interdependencies. That is, besides some cases in which discrete-event simulation can e.g. be replaced with queuing theory.
Phases of simulation-based intralogistics planning
The figure below shows the typical phases of intralogistics planning that simulation modeling is applicable to. In general, availability and transparency of data, as well as clarity of requirements and system specifications, increase as planning stages become mature. That is, in the early stages, there is little to no data available.

This example model is mostly associated with the first phase, i.e. the design stage. In this stage, a simulation model aims to test layout variants and general concepts. Data quality and availability are poor, so I have to develop a model based on assumptions at this stage. For example, when planning a logistics unit for a new factory, there will be no data available on actual customer demand, supply schedules and production schedules. In other words, I have to develop and verify a layout and process logic that is reasonably good when assessed under a large degree of uncertainty. In the conveyor simulation model presented in this article, for example, I thus modeled product-group specific stochastic demand patterns and supply lead times. This makes the results generalizable, i.e. valid for not just one specific production schedule but rather an entire category of schedule types.
Model overview of conveyor simulation in AnyLogic
Below is a screenshot that provides an overview of the AnyLogic conveyor simulation I created. The model itself is an example that can be adapted to a specific case.

Any industrial conveyor network of this kind will potentially involve a number of other pieces of equipment beyond conveyors. For example, a system of this kind could be interfacing with cranes, AGVs, or manually operated forklifts. The model, however, only comprises conveyors and turn tables. Again, this is due to the nature of the early stages of facility planning projects. As the availability of data is not high and many aspects of the overall system are unclear, it is important to focus on a specific aspect for further analysis. In this case, the model can compare competing layout variants for the conveyor network and different routing concepts for operating them. All of this is subject to general assumptions, describing e.g. pick times at conveyor exit points and buffer dwell times for connected storage areas.
Core components of the AnyLogic conveyor simulation
The conveyor simulation model consists of the following main components:
Conveyor network connecting feeding processes (“receiving”) with buffer areas and production/shipping areas (“processing”)
A routing concept, implemented as a routing function in JAVA
Functions, parameters and variables for setting initial buffer fill levels, and for updating these throughout the simulation run
Stochastic model describing system input, i.e. simulated production or supply schedules
Statistics for visualizing buffer fill degree, utilization of critical turn tables, and conveyor system throughput
Stochastic demand patterns and supply schedules allow for modeling peaks and valleys, reflecting different production and logistics scenarios. When supply rates are high, the buffer fill rates generally increase. Vice versa, a peak in demand and/or low supply rates increase relative buffer outflow, resulting in declining fill rates. The chart below represents a timespan in the simulation where buffer fill rates are declining due to excessive customer orders. Largely, these are supplied by the buffer area.

At another point in time, the fill rate increases as supply from upstream production, assembly and supply processes exceed shipping volumes toward customers on the output side. This is shown in the chart below.

Lastly, there are periods during which the filling rates oscillate within a range. As in the other cases, this reflects volatility on both the input and output side.

As can be seen from the above charts, the relative fill rate of both buffer areas is always relatively equal. That is due to active balancing. That balancing operation is one core aspect of the routing logic. Vice versa, fill rate balancing also means that the probability of retrieving parts from the buffer decreases as the fill rates decline. That is because fewer parts are being stored in the buffer, and thus the specific part that has to be shipped to some specific customer is less likely to be located in the buffer and more likely to be produced in the upstream supply processes.
The routing concept (i.e. the “routing” function visible in the model space) is the most complex model component. This function dispatches tasks in the form of “part” agents and defines their route by specifying the source and sink conveyor. Below is a snapshot showing the content of the “part” agent class.

Usually, when implementing conveyor routing logic in a simulation model, I first draft the routing logic using mathematical programming. The figure below shows the procedure recommended by me for doing so. I covered this workflow in another article. You can find that article on my blog here. The key message here is that I do not immediately start with a conveyor simulation. Instead, I use mathematical programming to derive optimal routing ratios for the conveyor system. Calculation of these routing ratios is subject to simplifying assumptions, such as e.g. neglecting dynamic system behavior and interdependencies between system entities. Nevertheless, mathematically derived routing ratios provide a good starting point for a simulation. In fact, I strongly believe a solid routing concept is established more efficiently in this way. The alternative is to simulate conveyor system throughput with widely varying routing ratios or routing concepts, and the effort for doing so is very likely to be much higher.
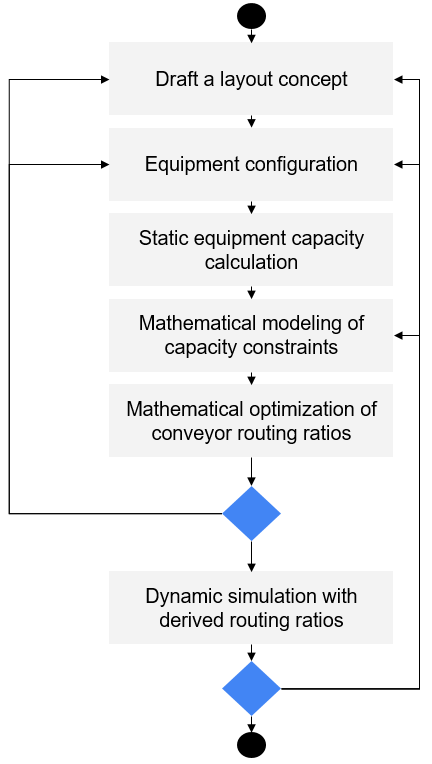
As already explained, the routing logic actively balances fill rates of both work areas. In addition, based on routing ratios derived from the mathematical program ahead of simulation modeling, the model facilitates random routing with defined probabilities for the various feasible routes throughout the conveyor network.
Simulation-based comparison of two layout variants
Having roughly explained the simulation model, I now use it to conduct a conveyor simulation. I start with the initial layout variant, as depicted in the model overview introduced at the beginning of this article. Some turntables in the conveyor network are located at critical positions (main routes and/or crossing material flows). I monitor their utilizations throughout the simulation.

The chart above tells me that while one of the three critical turntables is running at full utilization, the other tables still have some capacity. In fact, turntables no. 8 and no. 9 are critical in this case. Balancing their utilization will benefit overall system throughput. For this reason, I simulate a layout variant in which one of the retrieval conveyors (input-side) is located at a different position. Retrieval conveyor no. 3 is now connected directly to the vertical conveyor line in the center of the layout. This allows some of the parts supplied via this conveyor to be routed directly to the south via the vertical conveyor line, while some other parts can be routed e.g. to buffer area 2 via the Northern conveyor lines. You can see a snapshot from the 2D AnyLogic model taken during the simulation below.

Even better, the turntable utilization chart now confirms “nearly full” utilization of both turntables, i.e. turntables no. 8 and no. 9. See the chart below.

Consequently, system throughput increased by roughly 13%.
Summary
A discrete-event simulation model allows analysts and engineers to assess the impact of dynamic system behavior. A conveyor system can be drafted with static and analytical methods, i.e. rules-of-thumb and mathematical programming. However, dynamic simulation modeling must always assess the resulting layout draft. In this post, I use a simulation model developed in AnyLogic to evaluate an initial conveyor layout and design. While executing this process, I identified a bottleneck in the conveyor layout. Consequently, I adjusted the layout and confirmed layout improvements by means of additional simulation runs. This allowed me to identify the “best” layout subject to material flow volatility and associated risks. This is especially valuable in the earliest design phase. In this case, a minor relocation of an inlet conveyor increased total throughput capacity by 13%. Certainly, there might have been a solid technical reason for locating the bespoken inlet conveyor at its initial position. With a simulation model, however, it is possible to challenge such layout and design decisions with hard data and quantified findings. This leads to much better facility layouts and designs.
Although I only showed one possible variation, I could optimize the layout even further and subsequently use the simulation model to test the effect these layout changes have on total system performance.
For those interested in the model source code, please contact support@theanylogicmodeler.com for details.
Linnart Felkl
Linnart Felkl is a guest writer for the AnyLogic Modeler. Feel free to connect with him over LinkedIn. He also has a blog, Supply Chain Data Analytics, where he and a number of other writers, regularly post about various technologies used in analyzing supply chains as well as other related topics.
What next?
If you liked this post, you are welcome to read more posts by following the links above to similar posts. Why not subscribe to our blog or follow us on any of the social media accounts for future updates? The links are in the Menu bar at the top, or the footer at the bottom. You can also join the mobile app here!
If you want to contact us for some advice, maybe a potential partnership or project or just to say "Hi!", feel free to get in touch here, and we will get back to you soon!

Comments